Unsupervised Learning: PCA(Ⅱ)
本文主要从组件和SVD分解的角度介绍PCA,并描述了PCA的神经网络实现方式,通过引入宝可梦、手写数字分解、人脸图像分解的例子,介绍了NMF算法的基本思想,此外,还提供了一些PCA相关的降维算法和论文
Reconstruction Component
假设我们现在考虑的是手写数字识别,这些数字是由一些类似于笔画的basic component组成的,本质上就是一个vector,记做
写成表达式就是:
其中
比如7就是
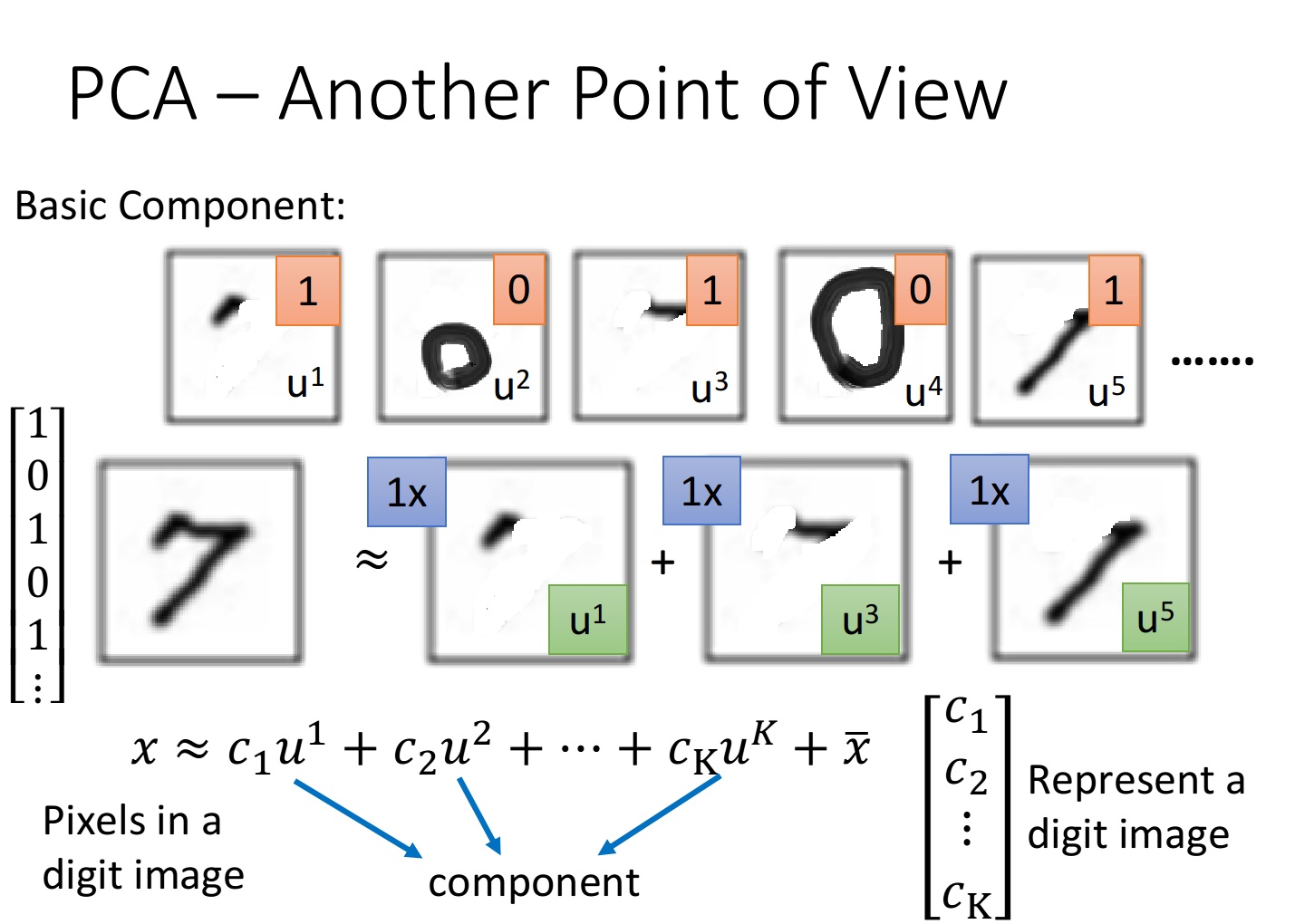
实际上目前我们并不知道
而用未知component来描述的这部分内容,叫做Reconstruction error,即
接下来我们就要去找k个vector
回顾PCA,
- 我们将所有的
都用下图中的矩阵相乘来表示,我们的目标是使等号两侧矩阵之间的差距越小越好
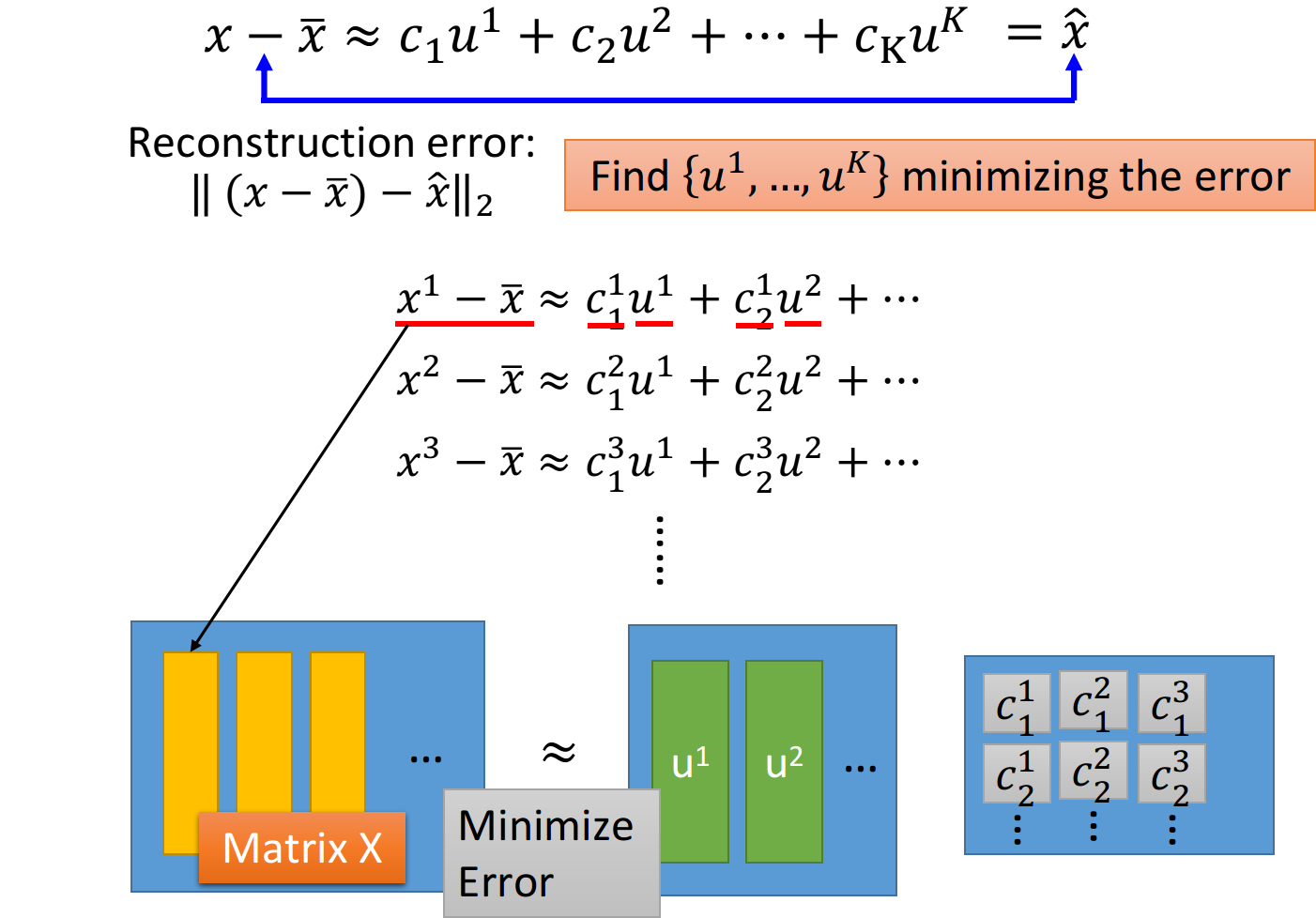
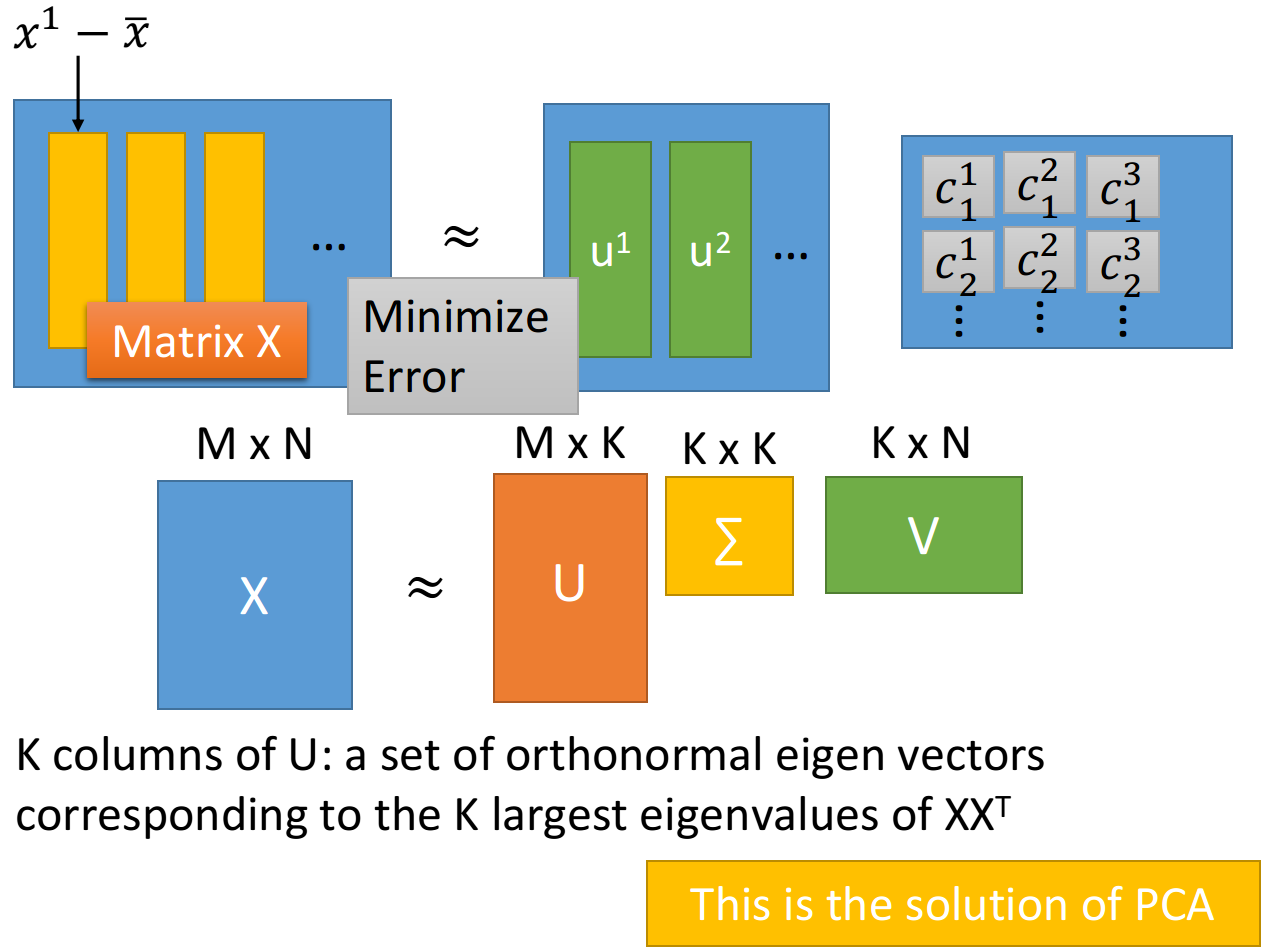
- 可以使用SVD将每个matrix
都拆成matrix 、 、 的乘积,其中k为component的数目 - 值得注意的是,使用SVD拆解后的三个矩阵相乘,是跟等号左边的矩阵
最接近的,此时 就对应着 那部分的矩阵, 就对应着 那部分的矩阵 - 根据SVD的结论,组成矩阵
的k个列向量(标准正交向量, orthonormal vector)就是 最大的k个特征值(eignvalue)所对应的特征向量(eigenvector),而 实际上就是 的covariance matrix,因此 就是PCA的k个解 - 因此我们可以发现,通过PCA找出来的Dimension Reduction的transform,实际上就是把
拆解成能够最小化Reconstruction error的component的过程,通过PCA所得到的 就是component ,而Dimension Reduction的结果就是参数 - 简单来说就是,用PCA对
进行降维的过程中,我们要找的投影方式 就相当于恰当的组件 ,投影结果 就相当于这些组件各自所占的比例
下面的式子简单演示了将一个样本点
划分为k个组件的过程,其中 是每个组件的比例;把 划分为k个组件即从n维投影到k维空间, 也是投影结果 注:
和 均为n维列向量
NN for PCA
现在我们已经知道,用PCA找出来的
而
在PCA中我们已经证得,
这个时候我们就可以使用神经网络来表示整个过程,假设
- 对
与 做inner product的过程类似于neural network, 在3维空间上的坐标就相当于是neuron的input,而 , , 则是neuron的weight,表示在 这个维度上投影的参数,而 则是这个neuron的output,表示在 这个维度上投影的坐标值;对 也同理
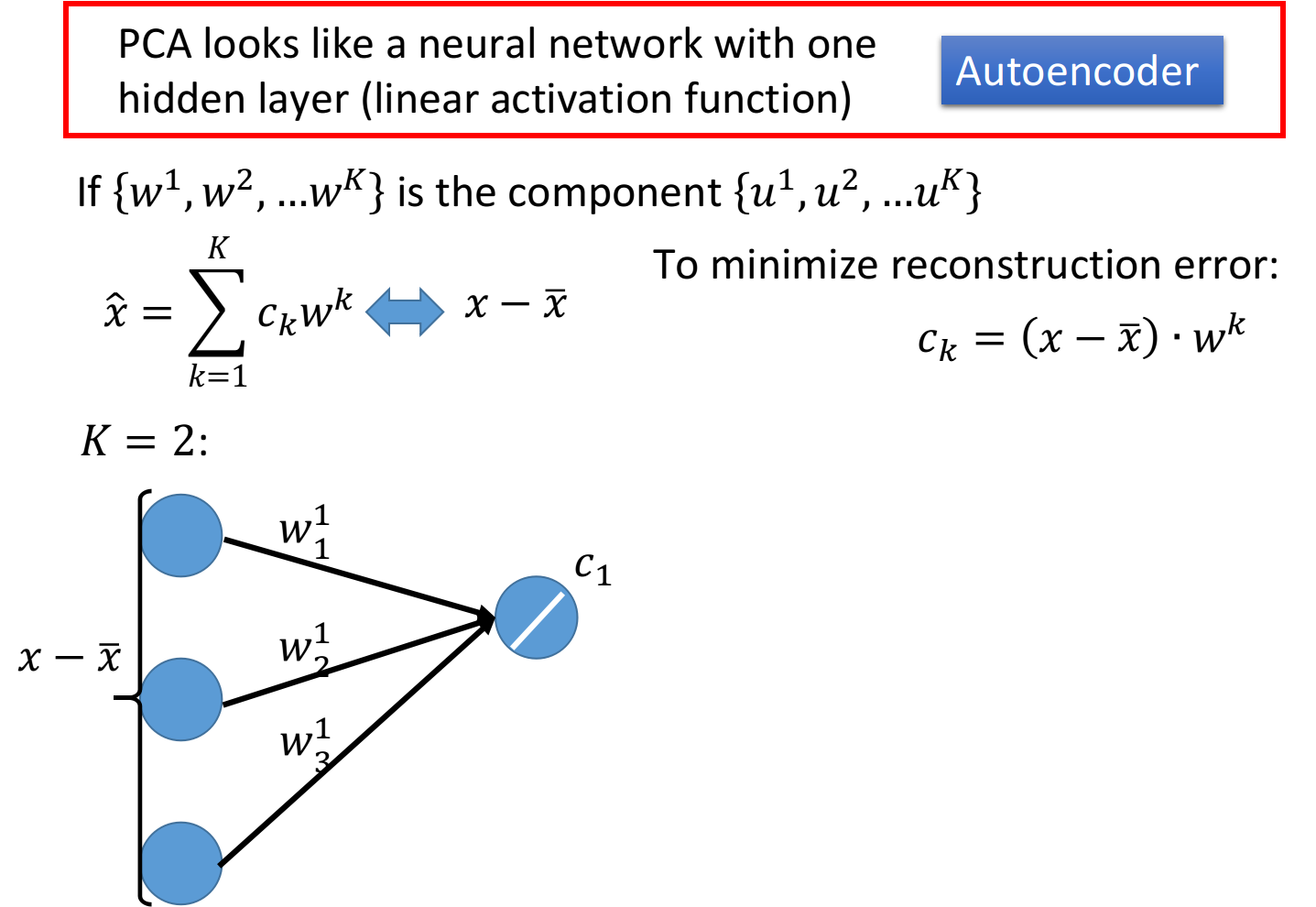
- 得到
之后,再让它乘上 ,得到 的一部分
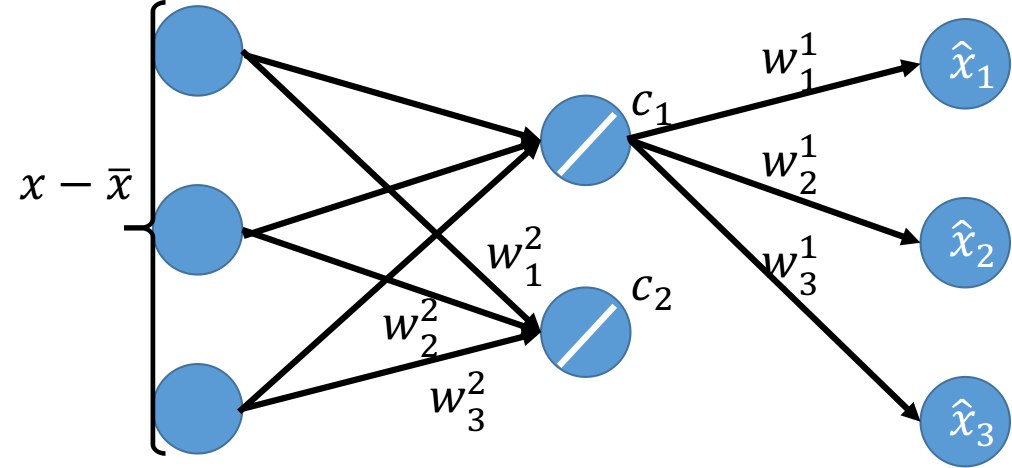
- 对
进行同样的操作,乘上 ,贡献 的剩余部分,此时我们已经完整计算出 三个分量的值

此时,PCA就被表示成了只含一层hidden layer的神经网络,且这个hidden layer是线性的激活函数,训练目标是让这个NN的input
与output 越接近越好,这件事就叫做Autoencoder 注意,通过PCA求解出的
与直接对上述的神经网络做梯度下降所解得的 是会不一样的,因为PCA解出的 是相互垂直的(orgonormal),而用NN的方式得到的解无法保证 相互垂直,NN无法做到Reconstruction error比PCA小,因此: - 在linear的情况下,直接用PCA找
远比用神经网络的方式更快速方便 - 用NN的好处是,它可以使用不止一层hidden layer,它可以做deep autoencoder
- 在linear的情况下,直接用PCA找
Weakness of PCA
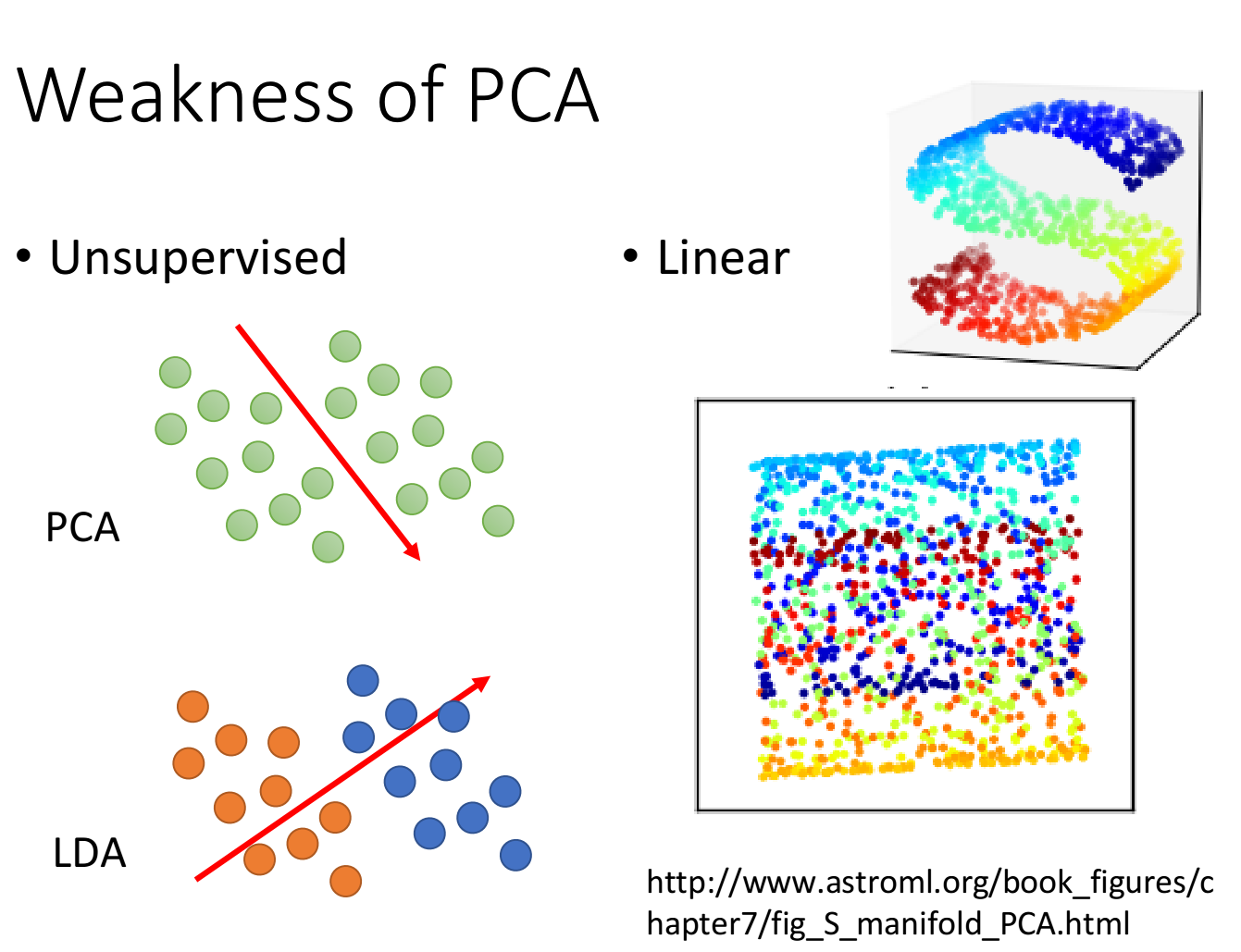
PCA有很明显的弱点:
它是unsupervised的,如果我们要将下图绿色的点投影到一维空间上,PCA给出的从左上到右下的划分很有可能使原本属于蓝色和橙色的两个class的点被merge在一起
而LDA则是考虑了labeled data之后进行降维的一种方式,但属于supervised
它是linear的,对于下图中的彩色曲面,我们期望把它平铺拉直进行降维,但这是一个non-linear的投影转换,PCA无法做到这件事情,PCA只能做到把这个曲面打扁压在平面上,类似下图,而无法把它拉开
对类似曲面空间的降维投影,需要用到non-linear transformation
PCA for Pokemon
这里举一个实际应用的例子,用PCA来分析宝可梦的数据
假设总共有800只宝可梦,每只都是一个六维度的样本点,即vector={HP, Atk, Def, Sp Atk, Sp Def, Speed},接下来的问题是,我们要投影到多少维的空间上?
如果做可视化分析的话,投影到二维或三维平面可以方便人眼观察
实际上,宝可梦的

从上图的ratio可以看出
注意到新的维度本质上就是旧的维度的加权矢量和,下图给出了前4个维度的加权情况,从PC1到PC4这4个principle component都是6维度加权的vector,它们都可以被认为是某种组件,大多数的宝可梦都可以由这4种组件拼接而成,也就是用这4个6维的vector做linear combination的结果
我们来仔细分析一下这些组件:
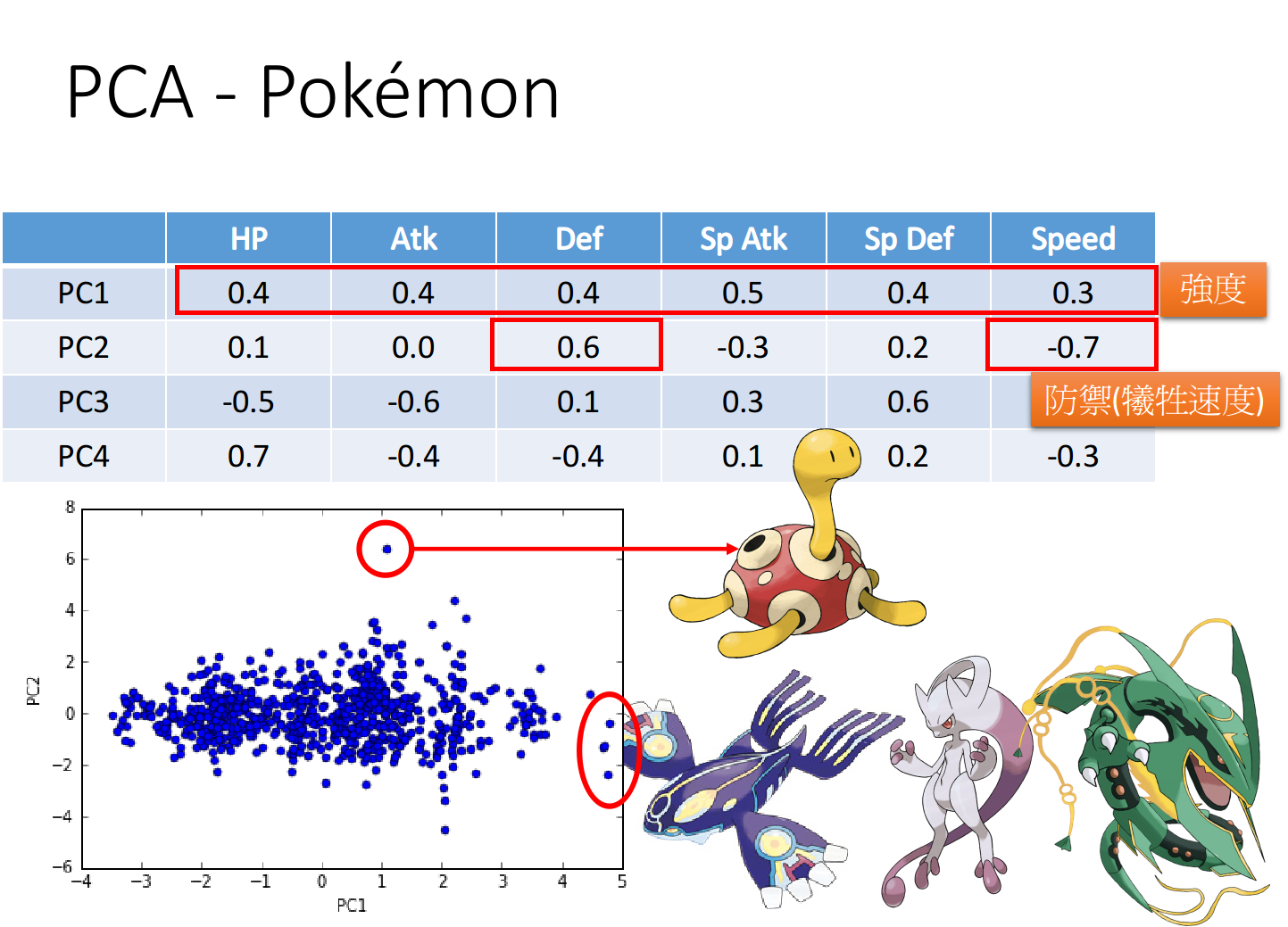
对第一个vector PC1来说,每个值都是正的,因此这个组件在某种程度上代表了宝可梦的强度
对第二个vector PC2来说,防御力Def很大而速度Speed很小,这个组件可以增加宝可梦的防御力但同时会牺牲一部分的速度
如果将宝可梦仅仅投影到PC1和PC2这两个维度上,则降维后的二维可视化图像如下图所示:
从该图中也可以得到一些信息:
- 在PC2维度上特别大的那个样本点刚好对应着普普(海龟),确实是防御力且速度慢的宝可梦
- 在PC1维度上特别大的那三个样本点则对应着盖欧卡、超梦等综合实力很强的宝可梦
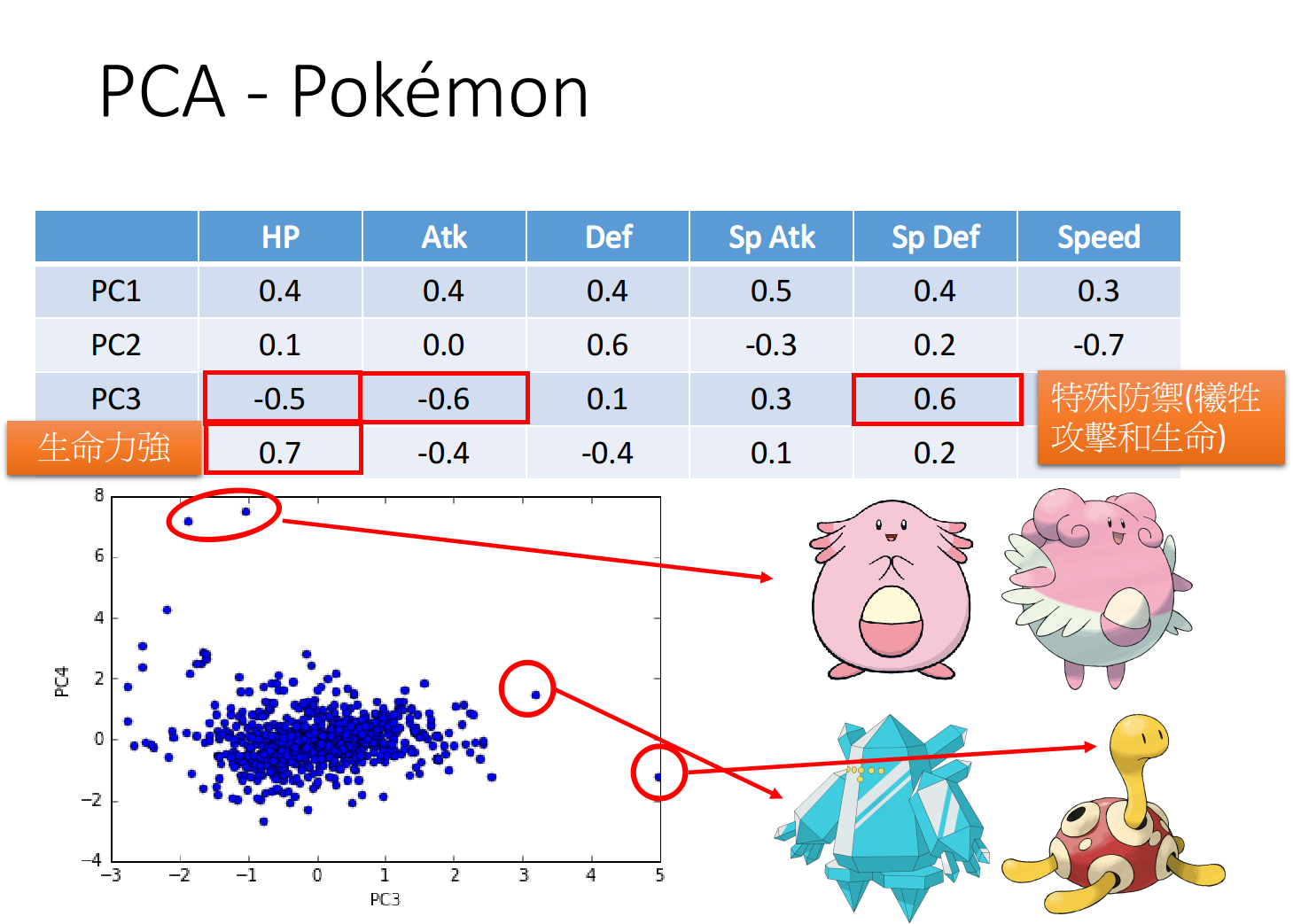
对第三个vector PC3来说,sp Def很大而HP和Atk很小,这个组件是用生命力和攻击力来换取特殊防御力
对第四个vector PC4来说,HP很大而Atk和Def很小,这个组件是用攻击力和防御力来换取生命力
同样将宝可梦只投影到PC3和PC4这两个维度上,则降维后得到的可视化图像如下图所示:
该图同样可以告诉我们一些信息:
- 在PC3维度上特别大的样本点依旧是普普,第二名是冰柱机器人,它们的特殊防御力都比较高
- 在PC4维度上特别大的样本点则是吉利蛋和幸福蛋,它们的生命力比较强
PCA for MNIST
再次回到手写数字识别的问题上来,这个时候我们就可以熟练地把一张数字图像用多个组件(维度)表示出来了:
这里的
注:PCA就是求

PCA for Face
同理,通过PCA找出人脸的前30个组件(维度),如下图所示:
用这些脸的组件做线性组合就可以得到所有的脸

What happens to PCA
在对MNIST和Face的PCA结果展示的时候,你可能会注意到我们找到的组件好像并不算是组件,比如MNIST找到的几乎是完整的数字雏形,而Face找到的也几乎是完整的人脸雏形,但我们预期的组件不应该是类似于横折撇捺,眼睛鼻子眉毛这些吗?
如果你仔细思考了PCA的特性,就会发现得到这个结果是可能的
注意到linear combination的weight
NMF
Introduction
如果你要一开始就得到类似笔画这样的基础组件,就要使用NMF(non-negative matrix factorization),非负矩阵分解的方法
PCA可以看成对原始矩阵
而NMF的基本精神是,强迫使所有组件和它的加权值都必须是正的,也就是说所有图像都必须由组件叠加得到:
- Forcing
, ...... be non-negative - additive combination
- Forcing
, ...... be non-negative - More like “parts of digits”
注:关于NMF的具体算法内容可参考paper(公众号回复“NMF”获取pdf):
Daniel D. Lee and H. Sebastian Seung. "Algorithms for non-negative matrix factorization."Advances in neural information processing systems. 2001.
NMF for MNIST
在MNIST数据集上,通过NMF找到的前30个组件如下图所示,可以发现这些组件都是由基础的笔画构成:

NMF for Face
在Face数据集上,通过NMF找到的前30个组价如下图所示,相比于PCA这里更像是脸的一部分

More Related Approaches
降维的方法有很多,这里再列举一些与PCA有关的方法:
Multidimensional Scaling (MDS) [Alpaydin, Chapter 6.7]
MDS不需要把每个data都表示成feature vector,只需要知道特征向量之间的distance,就可以做降维,PCA保留了原来在高维空间中的距离,在某种情况下MDS就是特殊的PCA
Probabilistic PCA [Bishop, Chapter 12.2]
PCA概率版本
Kernel PCA [Bishop, Chapter 12.3]
PCA非线性版本
Canonical Correlation Analysis (CCA) [Alpaydin, Chapter 6.9]
CCA常用于两种不同的data source的情况,比如同时对声音信号和唇形的图像进行降维
Independent Component Analysis (ICA)
ICA常用于source separation,PCA找的是正交的组件,而ICA则只需要找“独立”的组件即可
Linear Discriminant Analysis (LDA) [Alpaydin, Chapter 6.8]
LDA是supervised的方式
